淺談C語言中的浮點數
時間：2018-09-25 來源：未知
在C語言中用于存儲浮點數的有兩種類型，單精度float和雙精度double。我們知道整形數據或者字符型數據在計算機中存儲的是該數據所對應的補碼。那么浮點數在計算機中如何存儲的呢。無論是單精度還是雙精度在存儲中都分為三個部分：
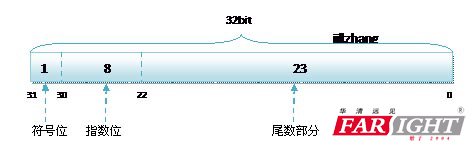
1 符號位(Sign) : 0代表正，1代表為負(即浮點數沒有無符號的)
2 指數位(Exponent):用于存儲科學計數法中的指數數據，并且采用移位存儲(注意指數位是指數移位得到的數這部分與取值范圍有關)
3 尾數部分(Mantissa)：尾數部分(與有效位數有關)
其中float的存儲方式如下圖所示：
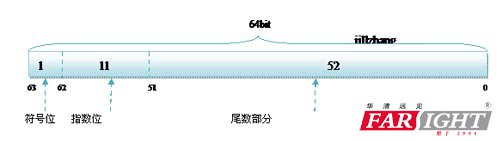
而雙精度的存儲方式為:
在分析浮點數的存儲是有兩個比較重要的概念需要搞清楚：1.有效位數、2.取值范圍。
1：有效位數：
單精度數的尾數用23位存儲，加上默認的小數點前的1位1，2^(23+1) = 16777216。因為 10^7 < 16777216 < 10^8，所以說單精度浮點數的有效位數是7位。雙精度的尾數用52位存儲，2^(52+1) = 9007199254740992，10^16 < 9007199254740992 < 10^17，所以雙精度的有效位數是16位。
2：取值范圍：
要搞清楚浮點數的取值范圍必須了解指數位存儲的是什么，float中指數位=128+指數，double中指數位= 1024+指數。那么float中指數的范圍是-127-128。Double中指數的范圍是-1023-1024。那么float的取值范圍是-2^128–2^128 即-3.4E+38–3.4E+38double的取值范圍-1.79E+308-1.79E+308.
下面我們來驗證一下：
我們可以將浮點數寫到計算機中，然后去內存中看看浮點數如何存儲。當然這種方式不是什么情況都適用，因為在有些情況下我們沒有辦法查看內存。那么我們可以反向思維的方式去驗證。即將浮點數按照浮點數的格式存儲的內存中。然后按照浮點數的方式讀取出來，與之前的浮點數對比。若相同則可驗證。
例：
浮點數5.5 二進制形式為101.1
轉化為浮點數存儲格式為：0 10000001 0110000000000000000
符號 指數位 尾數部分
即：0x40b00000
下面是C語言程序：
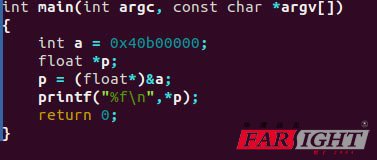
運行結果為：
